Page 146 - ATA YAYINCILIK 8. Sınıf Ben Korkmam Matematik Soru Bankası
P. 146
CEBİRSEL İFADELER VE ÖZDEŞLİKLER
ÖZDEŞLİKLERİ MODELLEME
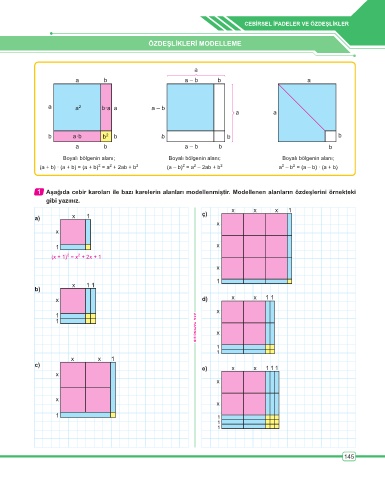
a
a b a – b b a
a a 2 b·a a a – b
a a
b a·b b 2 b b b b
a b a – b b b
Boyalı bölgenin alanı; Boyalı bölgenin alanı; Boyalı bölgenin alanı;
2
2
2
2
2
2
(a + b) · (a + b) = (a + b) = a + 2ab + b 2 (a – b) = a – 2ab + b 2 a – b = (a – b) · (a + b)
1 Aşağıda cebir karoları ile bazı karelerin alanları modellenmiştir. Modellenen alanların özdeşlerini örnekteki
gibi yazınız.
x x x 1
ç)
a) x 1
x
x
1 x
2
2
(x + 1) = x + 2x + 1
x
1
x 1 1
b)
x d) x x 1 1
x
1
1
x
1
1
x x 1
c) e) x x 1 1 1
x
x
x
x
1 1
1
1
145